Substring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved. In this context, the terms string and sequence have the same meaning.
Contents |
Subsequence
- Main article subsequence
A subsequence of a string 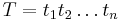 is a string
is a string 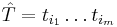 such that
such that  , where
, where 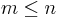 . Subsequence is a generalisation of substring, suffix and prefix. Finding the longest string which is equal to a subsequence of two or more strings is known as the longest common subsequence problem.
. Subsequence is a generalisation of substring, suffix and prefix. Finding the longest string which is equal to a subsequence of two or more strings is known as the longest common subsequence problem.
Example: The string anna is equal to a subsequence of the string banana:
banana || || an na
Including the empty subsequence, the number of subsequences of a string of length  where symbols only occur once, is simply the number of subsets of the symbols in the string, i.e.
where symbols only occur once, is simply the number of subsets of the symbols in the string, i.e. 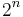 .
.
Substring
A substring (or factor) of a string 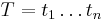 is a string
is a string 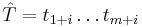 , where
, where 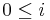 and
and 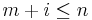 . A substring of a string is a prefix of a suffix of the string, and equivalently a suffix of a prefix. If
. A substring of a string is a prefix of a suffix of the string, and equivalently a suffix of a prefix. If 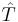 is a substring of
is a substring of  , it is also a subsequence, which is a more general concept. Given a pattern
, it is also a subsequence, which is a more general concept. Given a pattern  , you can find its occurrences in a string
, you can find its occurrences in a string  with a string searching algorithm. Finding the longest string which is equal to a substring of two or more strings is known as the longest common substring problem.
with a string searching algorithm. Finding the longest string which is equal to a substring of two or more strings is known as the longest common substring problem.
Example: The string ana is equal to substrings (and subsequences) of banana at two different offsets:
banana ||||| ana|| ||| ana
In the mathematical literature, substrings are also called subwords (in America) or factors (in Europe).
Not including the empty substring, the number of substrings of a string of length  where symbols only occur once, is the number of ways to choose two distinct places between symbols to start/end the substring. Including the very beginning and very end of the string, there are
where symbols only occur once, is the number of ways to choose two distinct places between symbols to start/end the substring. Including the very beginning and very end of the string, there are 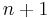 such places. So there are
such places. So there are 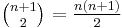 non-empty substrings.
non-empty substrings.
Prefix
A prefix of a string 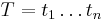 is a string
is a string 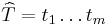 , where
, where 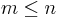 . A proper prefix of a string is not equal to the string itself (
. A proper prefix of a string is not equal to the string itself (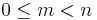 );[1] some sources[2] in addition restrict a proper prefix to be non-empty (
);[1] some sources[2] in addition restrict a proper prefix to be non-empty (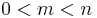 ). A prefix can be seen as a special case of a substring.
). A prefix can be seen as a special case of a substring.
Example: The string ban is equal to a prefix (and substring and subsequence) of the string banana:
banana ||| ban
The square subset symbol is sometimes used to indicate a prefix, so that 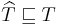 denotes that
denotes that 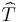 is a prefix of
is a prefix of  . This defines a binary relation on strings, called the prefix relation.
. This defines a binary relation on strings, called the prefix relation.
In formal language theory, the term prefix of a string is also commonly understood to be the set of all prefixes of a string, with respect to that language. See the article on string functions for more details.
Suffix
A suffix of a string 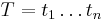 is a string
is a string 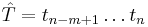 , where
, where 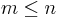 . A proper suffix of a string is not equal to the string itself (
. A proper suffix of a string is not equal to the string itself (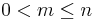 ); again, a more restricted interpretation is that it is also not empty[1] (
); again, a more restricted interpretation is that it is also not empty[1] (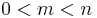 ). A suffix can be seen as a special case of a substring.
). A suffix can be seen as a special case of a substring.
Example: The string nana is equal to a suffix (and substring and subsequence) of the string banana:
banana |||| nana
Border
A border is suffix and prefix of the same string, e.g. "bab" is a border of "babab".
Superstring
Given a set of  strings
strings 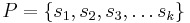 , a superstring of the set
, a superstring of the set  is single string that contains every string in
is single string that contains every string in  as a substring. For example, a concatenation of the strings of
as a substring. For example, a concatenation of the strings of  in any order gives a trivial superstring of
in any order gives a trivial superstring of  . For a more interesting example, let
. For a more interesting example, let 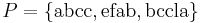 . Then
. Then 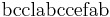 is a superstring of
is a superstring of  , and
, and 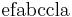 is another, shorter superstring of
is another, shorter superstring of  . Generally, we are interested in finding superstrings whose length is small.
. Generally, we are interested in finding superstrings whose length is small.